오늘은 차단기의 용량 선정시에 중요한 포인트 중 하나인
정격차단용량 (정격차단전류)를 선정해 보려고 합니다.
그럼 정격차단용량 (정격차단전류)을 선정할때 필요한 고장전류 계산법에 대하여 이야기 해 보겠습니다.
차단기를 설계할때 정격전압, 정격용량, 정격전류등과 함께 가장 중요한 요소 중에 하나가 바로 이
'정격차단전류 (정격차단용량)' 입니다.
차단기에게 있어 정격차단전류의 값이 가지는 의미는 선로나 전기회로상에 사고가 났을경우
회로 및 선로에 흐르게 되는 거대한 고장전류를 신속하고 안전하게 차단할 수 있는 한계치를 의미합니다.
(만약 계산을 잘못하여 차단기의 정격차단용량보다
큰 고장전류가 흐를경우 차단기가 정상작동하지 못하고
사고가 확산되어 설비에 막대한 피해를 입게 됩니다.
그렇기 때문에 굉장히 중요한 사항임을 명심해야 합니다.)
위와 같은 사항때문에 정격차단용량을 산정하는 작업은 굉장히 중요한 작업입니다.
어찌보면 앞전 포스팅을 통해 알아보았던 평상시 부하전류를 안전하게 통전하기 위한 차단기 용량 보다도
더 중요한 내용입니다.
먼저 일반적인 차단기 용량선정에 대한 내용은 아래 포스팅을 참조해 주십시오.
#1 분기회로
분기회로 (저압) 차단기 용량 선정
이번 포스팅에서는 분기회로에서 최종 말단 부하를 직접 보호하기 위해 설치되는 저압 분기회로 차단기의 용량을 선정하는 방법을 이야기해 보겠습니다. 차단기 용량선정 과 케이블 사이즈
mech19.tistory.com
#2 간선
간선 차단기 용량 / 케이블 사이즈 (전선 굵기) 선정 #1
이번시간에는 간선의 차단기 용량과 케이블 사이즈 (전선 굵기)에 대해서 알아보겠습니다. 간선은 여러개의 분기회로가 모여 더 많은 전력을 전달하는 분기회로 상위단의 회로를 의미합니다.
mech19.tistory.com
(너무 높은 정격차단전류를 선정하면 비용이 낭비되고,
너무 낮은 정격차단전류를 선정하면 사고의 전파를 막지못해 엄청난 손실을 입게 되겠지요...)
그럼 먼저 사고의 종류에 대해 알아보겠습니다.
1. 사고의 종류
사고의 종류에는 크게 지락사고와 단락사고가 있습니다.
1) 지락사고
지락사고란 선로나 회로의 케이블이 끊어지거나 케이블의 지지대가 부서져서 케이블이 직접적으로
혹은 구조물이나 건축물등을 통해 간접적으로 대지와 연결되는 상태가 되는 사고를 의미하며,
케이블 한가닥이 지락되는 1선지락, 케이블 두가닥이 지락되는 2선지락등이 있습니다.
2) 단락사고
단락사고란 선로나 회로의 케이블이 서로 맞닿아져서 연결되는 상태가 되는 사고를 의미 하며,
2상이 단락되는 2선단락, 3상이 단락되는 3상단락 등이 있습니다.
3) 평형고장, 불평형고장
1선지락과 2선지락, 그리고 2선단락사고는 불평형 고장이고, 3상단락사고는 평형고장 입니다.
이에 불평형 고장의 경우는 대칭좌표법을 사용하여 고장계산을 하며, 평형고장일 때는 %Z법을 주로 사용합니다.
우리가 고장계산을 하는 주 목적은 차단기 선정시에 정격차단전류(정격차단용량)을 구하기 위해서 입니다.
그런데 여러가지 사고 중에서 보통 3상단락 사고시의 고장전류가 가장 크기때문에 해당 단락전류를 기준으로
정격차단전류(정격차단용량)을 선정합니다.
2. 고장계산의 종류
고장계산의 방법에는 옴법, %Z법(PU법), 대칭좌표법, 클라크법 등이 있습니다.
이중에서 우리는 고장전류의 크기가 가장 큰 3상단락사고시에 발생하는 단락전류의 크기를 계산해야하고
3상단락사고는 평형 사고이므로 %Z법(PU법)을 주로 사용하는데
옴법과의 비교를 통해 %Z법을 주로 사용하는 이유와 편리함에 대해 알아보고,
동시에 더 나아가서 실무적인 측면에서 고장계산하는 방법에 대해서 알아보도록 하겠습니다.
3. 옴법
옴법은 선로상의 실제 임피던스들을 모두 더해서 단락전류를 구하는 방법입니다.
단락전류를 구하는 공식은 옴의 법칙인 V = IR과 크게 다르지 않습니다.
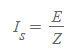
여기서 Is는 단락전류, E는 기준전압, Z는 선로의 임피던스입니다.
(여기서 Z를 왜 부하의 임피던스를 제외하고 선로의 임피던스만 고려하냐면,
케이블이 단락되면 케이블에 흐르는 전류가 부하까지 도달하지 못하고 다시 돌아가기 때문에
부하의 임피던스는 제외되는 것입니다.)
그런데 선로에 보면 발전소의 발전기에서 부터 우리가 사용하는 부하까지 오는 경로상에
여러가지 변압기가 존재합니다.
그래서 각 임피던스를 합상해주기 전에 권수비 환산 과정을 통해 기준전압에 맞는 임피던스로
환산시켜 주어야 합니다. (환산시켜주어야 하는 이유는 아래에 나와 있습니다.)
권수비를 a라고 할때 권수비와 전압, 전류, 임피던스이 관계는 아래와 같습니다.

따라서

이므로, 변압기를 기준으로 전압이 V1, V2로 나뉘게 되면 V2측의 임피던스를 V1측의 임피던스로 환산하려면
아래와 같이 a^2을 V2측의 임피던스에 곱해주어야 합니다.
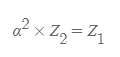
또한 V1측의 임피던스를 V2측의 임피던스로 환산하려면 아래와 같이 a^2로 V1측의 임피던스를
나누어 주어야 합니다.

이 내용을 잘 살펴보면 1차측 전압이 높고, 2차측 전압이 낮을 경우 V=IR이라는 옴의 법칙을 통해
R= V / I 가 되므로,
전압이 높고 전류가 낮으면 R값이 커지고,
전압이 낮고 전류가 높으면 R값이 작아진다는 것을 알 수 있습니다.
즉 리얼 임피던스 값은 권수비 환산 과장을 거치면, (1차측이 전압이 높고, 2차측 전압이 낮을 경우에 한함.)
1차측 기준으로는 임피던스가 커지고, 2차측 기준으로는 임피던스가 작아집니다.
(그렇게 때문에 임피던스를 기준전압을 기준으로 환산시켜 줄 필요가 있는 것입니다.)
4. %Z법 (퍼센트 임피던스 법)
이제 %Z법에 대해 알아보겠습니다.
%Z법은 먼저 기준이 되는 임피던스가 있어야 합니다.
기준이 되는 기준 임피던스가 필요한 이유는
전체 임피던스 중에 사고가 난 선로의 임피던스가
비율적으로 얼마만큼을 차지하는지를 보여주려면 기준 필요하기 때문입니다.
이것을 수식으로 나타낸다면 아래와 같습니다.

위와 같이 line과 load의 임피던스 전체합이 기준임피던스가 되며
단락 사고가 발생하면 load의 임피던스가 제외가 된다는 개념입니다.
실제로 주어지는 파라미터를 이용하여 %Z를 구하는 방법은 아래와 같습니다.

여기서 In은 정격전류, Z는 선로나 변압기등 %Z를 구하고자 하는 설비의 임피던스이며,
E는 In이 흐를때의 정격전압을 의미합니다.
또한 PE와 PV는 각각 상전압일때의 피상전력과 선간전압일때의 피상전력값을 의미합니다.
이렇게 구한 %Z를 이용하여 단락전류를 계산하는 방법은 아래와 같습니다.
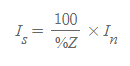
위의 수식은 정격전류와 단락전류간의 비율을 나타내는 것과 같습니다.
위의 수식은 아래의 옴의 법칙을 이용하여 유도해 낼 수 있다는 것을 기억해야 합니다.

먼저 변압기를 모델로 생각해 보자. E는 변압기의 정격전압이 될것이고, Z는 변압기의 임피던스를 의미합니다.
여기에 %Z를 구하는 식을 이용해 Z를 구해 볼 수 있습니다. 아래 수식을 참고해 주십시오.

을 변경해보면

이 되는데 이 %Z는 변압기의 %Z이므로 E와 In의 기준이 동일해야 함을 기억해야 합니다.
즉, In을 구할때의 기준용량과 기준전압과 E의 전압이 동일해야 한다는 것입니다.
다음 포스팅에서는 직접 예시회로를 이용하여 계산해보려고 합니다.
회로가 복잡해짐에 따라 %Z로 각각의 임피던스를 환산 후 합성하여
합성 %Z를 구하는 것이 훨씬 편리한것을 알 수 있게 될겁니다.
옴법을 이용할 경우 중간중간 변압기등의 존재로 전압이 변경되어 단순 저항값 합산이 불가능 하기 때문에
고장점의 기준전압값을 기준으로 권수비 환산을 하여 리얼 임피던스 값을 환산해 주어야
합산이 가능하다는 점을 잊지말아야 합니다.
오늘은 여기까지 이야기를 하고 마무리를 하겠습니다.
다음 포스팅에서 실제로 예를 들어 계산해 보겠습니다.
먼저 %Z법과 옴법을 실제로 예시를 통해 비교한 내용은 아래 포스팅을 참조해 주십시오.
차단기 용량 선정 - 고장계산 #2
오늘은 차단기를 선정하는 과정에서 아주 중요한 정격차단용량(정격차단전류)을 계산해 보려고 합니다. 예전에 이 내용에 대한 이론을 포스팅한 적이 있습니다. (아래 포스팅 참조) https://mech19.t
mech19.tistory.com
감사합니다.
'전기 > 전기 설계' 카테고리의 다른 글
| 차단기 용량 선정 - 고장계산 #3 (0) | 2021.12.15 |
|---|---|
| 차단기 용량 선정 - 고장계산 #2 (0) | 2021.12.15 |
| 간선 차단기 용량 / 케이블 사이즈 (전선 굵기) 선정 #2 (3) | 2021.03.25 |
| 간선 차단기 용량 / 케이블 사이즈 (전선 굵기) 선정 #1 (0) | 2021.03.24 |
| 분기회로 (저압) 차단기 용량, 케이블 사이즈 (전선굵기) 설계 (9) | 2021.03.19 |




댓글